VINCIA Shower Parameters

Main On/Off Switch

flag Vincia (default = on)
Main switch for VINCIA antenna showers. When set to on and the VINCIA plug-in is linked correctly to PYTHIA 8 (see section on installation and linking and/or the example program vincia01.cc included with the VINCIA plug-in), PYTHIA will use the VINCIA showers instead of its internal ones. If set to off instead, PYTHIA will use its own internal showers, regardless of whether the VINCIA plug-in is linked (useful for quick comparisons).

Conventions

Within the dipole-antenna formalism, antenna functions are the analogs of the splitting functions used in traditional parton showers. The antenna functions are constructed so as to reproduce the Altarelli-Parisi splitting functions P(z) in collinear limits and the eikonal dipole factor in the soft limit.

We here describe the parameters and switches used to control VINCIA's final-state and initial-state showers, including coupling and colour factors, helicity dependence, evolution (aka ordering or resolution) variables, the number of flavours allowed in gluon splittings during the shower evolution, kinematics maps (recoil strategy), and a few more options.

The notation s(i,j) (or equivalently s_ij) is reserved to always refer to the dot product defined by s(i,j) = 2 p_ip_j. Invariant masses are denoted by m, hence m²(i,j) = m_i² + m_j² + s(i,j).

We denote partons in the initial state by the first letters in the alphabet (a,b,...), and partons in the final final state by letters starting from i (i,j,k, ...). Capital letters are used for partons in the pre-branching (n-parton) state, while lower-case letters are used for partons in the post-branching state (with n+1 or n+2 partons). We emphasise that "pre" and "post" branching refers to the evolutionary sense, not time, which are only identical for final-state evolution. Thus, the following labeling conventions are adopted:

Final-Final (FF) branchings: I + K → i + j + k;
Initial-Final (IF) branchings: A + K + (B+R) → a + j + k + (B+r), where we allow for the possibility of recoil to a hard system R composed of one or more particlese whose combined momentum (but not invariant mass) may be changed by the branching. The label B refers to the non-participating other beam parton, whose momentum (x fraction) is not changed by the branching.
Initial-Initial (II) branchings: A + B + (R) → a + j + b + (r), where recoil is imparted to a hard system R composed of one or more particles whose combined momentum (but not invariant mass) is changed in the branching.
Resonance-Final (RF) branchings: A + K + (W) → A + j + k + (w), used for radiation in the antenna spanned between a (charged) decaying resonance and a final-state parton, for example the top-bottom antenna in t→bW; after the branching, the momentum of the on-shell decaying resonance is constrained to be unchanged (hence A is unchanged) but recoil is imparted to a system composed of one or more particles whose combined momentum (but not invariant mass) is changed in the branching.

The 2→3 (LL) VINCIA antennae have names such as

Vincia:QQEmitFF (for gluon emission off a final-final qqbar antenna),
Vincia:QGSplitIF (for gluon splitting to a quark-antiquark pair inside an initial-final qg antenna).

The generic name format is thus Vincia:ABxTT, where A and B are the "mothers" and x is emit, split, or conv depending on whether the process is gluon emission, gluon splitting (either in the initial or final state), or a gluon in the initial state backwards-evolving into a quark and emitting a quark into the final state (gluon conversion). TT can be either FF, IF, or FF, depending on whether the antenna in question is spanned between a final-final, initial-final, or initial-initial parton pair. For final-state antennae, the radiating (parent) antenna is always interpreted as spanned between the Les Houches colour tag of A and the anti-colour tag of B, see illustration to the right.

Common parameters affecting both ISR and FSR

The number of quark flavours allowed in final-state gluon splittings (in both FF and IF antennae) is given by

mode Vincia:nGluonToQuark (default = 5; minimum = 0; maximum = 5)
Number of allowed quark flavours in final-state gluon splittings, g → q qbar, during the shower evolution, phase space permitting. E.g., a change to 4 would exclude g → b bbar but would include the lighter quarks, etc. Note that this parameter does not directly affect the running coupling. Note also that quark mass effects are discussed separately, below.

Helicity Dependence

For each antenna function, a full set of helicity-dependent antenna function contributions are implemented. For partons without helicity information, the unpolarised forms (summed over post-branching helicities and averaged over pre-branching ones) are used. The detailed forms of both helicity and helicity-summed/averaged antenna functions are given in the VINCIA Authors' Compendium.

flag Vincia:helicityShower (default = on)
Switch to activate the helicity dependent showering (and matrix-element corrections) in VINCIA.

Mass Effects

mode Vincia:nFlavZeroMass (default = 4; minimum = 2; maximum = 6)
Controls the number of flavours that will be treated as massless by VINCIA, ie with massless kinematics and no mass corrections. The remaining flavours will be bookkept with massive kinematics and mass-corrected antenna functions. (Note: mass corrections are currently only available inside resonance-decay systems; outside of resonance decays, all partons are bookkept as massless.) Note that, even for flavours treated as massless, an elementary phase-space check is still made eg on all g→QQ branchings to ensure m(QQ) >= 2mQ. Likewise, all heavy flavours in the initial state are forced to undergo a conversion into a gluon when the evolution variable reaches their mass threshold (with the threshold determined by the maximum of the PDF threshold and the relevant user-specifiable mass parameter given below).

parm Vincia:ThresholdMB (default = 4.8)
threshold (mass, in GeV) for bottom quark production.

parm Vincia:ThresholdMC (default = 1.5)
for charm quark production.

Sector Showers

During the transition phase to full sector showers, the sector beahviour can be switched on or off using the following switch.

flag Vincia:sectorShower (default = off)
Switch to activate the sector shower (and matrix-element corrections) in VINCIA.

parm Vincia:sectorDamp (default = 0.0; minimum = 0.0; maximum = 1.0)
In the symmetrisation over post-branching gluons that is done to derive the sector antenna functions from the global ones, the branching invariant with swapped gluons is nominally given by yijSym = yik = 1 - yij - yjk. If the swapped gluons are j and k (and straightforwardly generalised if they are i and j) then the collinear yjk→0 limit does not change by adding or subtracting a term of order yjk. Therefore one could equally well use yijSym = 1 - yij (or something inbetween). This is still guaranteed to be positive definite and was indeed the choice in the original sector antenna shower papers. Since the latter definition produces a value for yijSym which is slightly larger than the former, the corresponding 1/yijSym singularities in the antenna function are damped slightly, so that larger values of the sectorDamp parameter produces sector antenna functions which have slightly smaller magnitudes outside the collinear limits. Strictly speaking this choice is an ambiguity that should be varied for uncertainty estimates, in which context we note that we expect it to be almost entirely degenerate with variations of nonsingular terms.

The Strong Coupling

Currently, the only SM parameter that can be configured in VINCIA is the definition of the strong coupling constant, specified by providing its reference value (interpreted as given at the Z pole in the MSbar scheme) and running properties (loop order, behaviour at top threshold, and any low-scale regularisation/dampening). All other parameters are taken from the PYTHIA Couplings database.

Note that VINCIA only uses one global value for the definition of the strong coupling constant. The effective couplings used in shower branchings (renormalisation scheme and scale) are governed by separate parameters which are specified under initial- and final-state showers respectively.

VINCIA implements its own instance of PYTHIA's AlphaStrong class for the strong coupling. You can find more documentation of the class in the section on Standard-Model Parameters in the PYTHIA documentation. Here, we list the specific parameters and switches governing its use in VINCIA.

The free parameter of the strong coupling constant is specified by

parm Vincia:alphaSvalue (default = 0.118; minimum = 0.06; maximum = 2.0)
The value of α_s at the scale m_Z, in the MSbar scheme. The default value is chosen to be in agreement with the current world average. The effective value used for showers may be further affected by translation to the CMW scheme (below) and by renormalisation-scale prefactors given for FSR and ISR showers separately.

mode Vincia:alphaSorder (default = 2; minimum = 0; maximum = 2)
Order at which α_s runs,
option 0 : zeroth order, i.e. α_s is kept fixed.
option 1 : first order, i.e., one-loop running.
option 2 : second order, i.e., two-loop running.

Resummation arguments [Cat91] indicate that a set of universal QCD corrections can be absorbed in coherent parton showers by applying the so-called CMW rescaling of the MSbar value of Lambda_QCD, defined by

α_s(CMW) = α_s(MSbar) * (1 + K * α_s(MSbar) / 2π) with K = CA * (67/18 - π²/6) - 5/9nf. The translation amounts to an NF-dependent rescaling of Lambda_QCD, relative to its MSbar value, by a factor 1.661 for NF=3, 1.618 for NF=4, 1.569 for NF=5, and 1.513 for NF=6. Although the original argument strictly concerned only the eikonal for soft-gluon emissions, the current version of VINCIA only offers the option of switching the rescaling of Lambda_QCD on or off, applied to all shower branchings.

flag Vincia:useCMW (default = true)
If set to on, the alphaS value used for shower branchings will be translated from the MSbar value to the CMW ("MC") scheme. If set to off, the MSbar value will be used.

Note 1: If using VINCIA with an externally defined matching scheme, be aware that the CMW rescaling may need be taken into account in the context of matrix-element matching. Note also that this option has only been made available for timelike and spacelike showers, not for hard processes.
Note 2: Tunes using this option need roughly 10% lower values of alpha_s(m_Z) than tunes that do not.

For both one- and two-loop running, the AlphaStrong class automatically switches from 3-, to 4-, and then to 5-flavour running as one passes the s, c, and b thresholds, respectively, with matching equations imposed at each flavour treshold to ensure continuous values. By default, a change to 6-flavour running is also included above the t threshold, though this can be disabled using the following parameter:

mode Vincia:alphaSnfmax (default = 6; minimum = 5; maximum = 6)

option 5 : Use 5-flavour running for all scales above the b flavour threshold (old default).
option 6 : Use 6-flavour running above the t threshold (new default).

parm Vincia:alphaSmuFreeze (default = 0.5; minimum = 0.0; maximum = 10.0)
The behaviour of the running coupling in the far infrared is regulated by a shift in the effective renormalisation scale, to μ_eff ² = μ_freeze² + μ_R².

parm Vincia:alphaSmax (default = 1.5; minimum = 0.1; maximum = 10.0)
Largest allowed numerical value for alphaS. I.e., the running is forced to plateau at this value.

Choice of Renormalisation Scales for Shower Branchings

When Vincia:alphaSorder is non-zero, the actual value of alphaS used for shower branchings is governed by the choice of scheme (MSbar or CMW, see the section on the choice of scheme (MSbar or CMW, see the section on AlphaStrong and then by running to the scale kR*muR², at which the shower evaluates α_s. The choice of functional form for muR is governed by

mode Vincia:renormType (default = 1; minimum = 0; maximum = 1)

option 0 : Renormalisation scale muR proportional to the evolution variable(s).
option 1 : Renormalisation scale muR proportional to pT for all branchings regardless of choice of evolution variable. The multiplicative scale factor kR is given by

parm Vincia:renormMultFacEmitF (default = 0.68; minimum = 0.1; maximum = 10.0)
for gluon emission

and

parm Vincia:renormMultFacSplitF (default = 0.6; minimum = 0.1; maximum = 10.0)
for gluon splitting.

For initial-state branchings, the functional form of muR is given by the evolution variable and the scale factor kR is given by

parm Vincia:renormMultFacEmitI (default = 0.72; minimum = 0.1; maximum = 10.0)
for gluon emission,

parm Vincia:renormMultFacSplitI (default = 0.72; minimum = 0.1; maximum = 10.0)
for gluon splitting (quark in the initial state backwards evolving into a gluon),

parm Vincia:renormMultFacConvI (default = 0.72; minimum = 0.1; maximum = 10.0)
for gluon conversion (gluon in the initial state backwards evolving into a (anti)quark)

Final-State Shower Parameters

flag Vincia:doFSR (default = on)
Main switch for final-state radiation on/off.

Colour Charge Factors

The normalisation of colour factors in VINCIA is chosen such that the coupling factor for all antenna functions is αS/4π. With this normalisation choice, all gluon-emission colour factors tend to NC in the large-NC limit while all gluon-splitting colour factors tend to unity. (Thus, e.g., the default normalisation of the qqbar → qgqbar antenna function is 2CF.)

parm Vincia:QQEmitFF:chargeFactor (default = 2.66666667)

parm Vincia:QGEmitFF:chargeFactor (default = 2.85)

parm Vincia:GGEmitFF:chargeFactor (default = 3.0)

parm Vincia:QGSplitFF:chargeFactor (default = 1.0)

parm Vincia:GGSplitFF:chargeFactor (default = 1.0)

parm Vincia:GXSplitFF:chargeFactor (default = 1.0)

parm Vincia:QQEmitRF:chargeFactor (default = 2.66666667)

parm Vincia:QGEmitRF:chargeFactor (default = 2.85)

parm Vinica:XGSplitRF:chargeFactor (default = 1.0)
Note: the two permutations g-g → g-q+qbar and g-g → qbar+q-g are explicitly summed over in the code (with appropriate swapping of invariants in the latter case).

Evolution Variable(s)

The choices below govern how the shower fills phase space, and hence how the logarithms generated by it are ordered. This does not affect the LL behaviour, but does affect the tower of higher (subleading) logs generated by the shower and can therefore be signficiant in regions where the leading logs are suppressed or absent. Note that, by construction, the antenna formalism automatically ensures an exact treatment of (leading-colour) coherence effects to leading logarithmic order, and hence additional constraints, such as angular ordering, are not required.

mode Vincia:evolutionType (default = 1; minimum = 1; maximum = 3)
Choice of functional form of the shower evolution variables (a.k.a. ordering variable), see illustrations below. By default, this choice applies to all branching types though see below for options to use a different evolution type for gluon splittings.
option 1 : Ordering in pT(j) = s(i,j) * s(j,k) / s(I,K). Since transverse momentum is roughly proportional to the inverse of the antenna function for gluon emission, it is in some sense the most natural evolution variable. It has also been shown to have the smallest NLO corrections. We define it as
option 2 : Ordering in pTmin = min(pT(j),pT(i),pT(k)). The pT of the softest parton with respect to the two others. Identical to option 1 in the phase-space region in which parton j is the softest parton.
option 3 : Ordering in virtuality. Defined as Dipole Virtuality for gluon emissions, min(sij,sjk), and m2qq for gluon splittings. This is as similar as it is possible to get to virtuality ordering for an antenna-like shower. The mass-like variable "dipole virtuality" represents a moderate variation on the transverse momentum. It will give slightly more priority to soft branchings over collinear branchings, as compared to transverse momentum.

mode Vincia:evolutionTypeSplit (default = 0; minimum = 0; maximum = 3)
Choice of evolution variable for g→qq splittings.
option 0 : Use the same evolution variable as for gluon emissions. I.e., use the choice defined by Vincia:evolutionType.
option 1 : Force evolution variable for g→qq to be pT(j) regardless of value of Vincia:evolutionType.
option 2 : Force evolution variable for g→qq to be pTmin regardless of value of Vincia:evolutionType.
option 3 : Force evolution variable for g→qq to be virtuality (mqq) regardless of value of Vincia:evolutionType.

Kinematics and Recoils

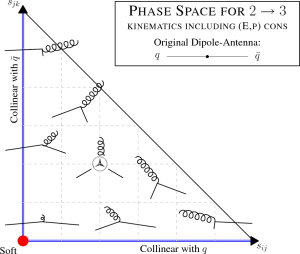
While the CM momenta of a 2→3 branching are fixed by the generated invariants (and hence by the antenna function), the global orientation of the produced 3-parton system with respect to the rest of the event (or, equivalently, with respect to the original dipole-antenna axis) suffers from an ambiguity outside the LL limits, which can affect the tower of subleading logs generated and can be significant in regions where the leading logs are suppressed or absent.

To illustrate this ambiguity, consider the emissision of a gluon from a qqbar antenna with some finite amount of transverse momentum (meaning transverse to the original dipole-antenna axis, in the CM of the dipole-antenna). The transverse momenta of the qqbar pair after the branching must now add up to an equal, opposite amount, so that total momentum is conserved, i.e., the emission generates a recoil. By an overall rotation of the post-branching 3-parton system, it is possible to align either the q or the qbar with the original axis, such that it becomes the other one that absorbs the entire recoil (the default in showers based on 1→2 branchings such as old-fashioned parton showers and Catani-Seymour showers), or to align both of them slightly off-axis, so that they share the recoil (the default in VINCIA, see illustration below).

mode Vincia:kineMapFFemit (default = 3; minimum = 1; maximum = 3)
Selects which method to use for choosing the Euler angle for the global orientation of the post-branching kinematics construction for gluon emissions.
option 1 : The ARIADNE angle (see illustration). The recoiling mothers share the recoil in proportion to their energy fractions in the CM of the dipole-antenna. Tree-level expansions of the VINCIA shower compared to tree-level matrix elements through third order in alphaS have shown this strategy to give the best overall approximation, followed closely by the KOSOWER map below.
option 2 : LONGITUDINAL. The parton which has the smallest invariant mass together with the radiated parton is taken to be the "radiator". The remaining parton is taken to be the "recoiler". The recoiler remains oriented along the dipole axis in the branching rest frame and recoils longitudinally against the radiator + radiated partons which have equal and opposite transverse momenta (transverse to the original dipole-antenna axis in the dipole-antenna CM). Comparisons to higher-order QCD matrix elements show this to be by far the worst option of the ones so far implemented, hence it could be useful as an extreme case for uncertainty estimates, but should probably not be considered for central tunes. (Note: exploratory attempts at improving the behaviour of this map, e.g., by selecting probabilistically between the radiator and the recoiler according to approximate collinear splitting kernels, only resulted in marginal improvements. Since such variations would introduce additional complications in the VINCIA matching formalism, they have not been retained in the distributed version.)
option 3 : The KOSOWER map. Comparisons to higher-order QCD matrix elements show only very small differences between this and the ARIADNE map above, but since the KOSOWER map is sometimes used in fixed-order contexts, we deem it interesting to include it as a complementary possibility. (Note: the KOSOWER maps in fact represent a whole family of kinematics maps. For experts, the specific choice made here corresponds to using r=sij/(sij+sjk) in the definition of the map.)

mode Vincia:kineMapFFsplit (default = 2; minimum = 0; maximum = 3)
Selects which method to use for choosing the Euler angle for the global orientation of the post-branching kinematics construction for gluon splittings.
option 1 : The ARIADNE angle (see illustration). The recoiling mothers share the recoil in proportion to their energy fractions in the CM of the dipole-antenna. Tree-level expansions of the VINCIA shower compared to tree-level matrix elements through third order in alphaS have shown this strategy to give the best overall approximation, followed closely by the KOSOWER map below.
option 2 : LONGITUDINAL. For gluon splittings, this choice forces the recoiler to always recoil purely longitudinally (in the antenna CM) regardless of the size of the branching invariants.
option 3 : The KOSOWER map. Comparisons to higher-order QCD matrix elements show only very small differences between this and the ARIADNE map above, but since the KOSOWER map is sometimes used in fixed-order contexts, we deem it interesting to include it as a complementary possibility. (Note: the KOSOWER maps in fact represent a whole family of kinematics maps. For experts, the specific choice made here corresponds to using r=sij/(sij+sjk) in the definition of the map.)

mode Vincia:kineMapRFemit (default = 1; minimum = 1; maximum = 2)
There is only one choice of kinematics map for resonance emissions. However there is a freedom to choose the recoiler(s).
option 1 : Takes all non-colour-connected daughters in the resonance decay system as the recoilers.
option 2 : Takes the original non-colour-connected daughter of the resonance to always take the full recoil. E.g. in t->bW the recoiler is always the W. This is equivalent to setting TimeShower:recoilToColoured = off for Pythia.

mode Vincia:kineMapRFsplit (default = 1; minimum = 1; maximum = 2)
Same as above, but for R-g splittings.
option 1 : Takes all non-colour-connected daughters in the resonance decay system as the recoilers.
option 2 : Takes the original non-colour-connected daughter of the resonance to always take the full recoil. E.g. in t->bW the recoiler is always the W. This is equivalent to setting TimeShower:recoilToColoured = off for Pythia.

Initial-State Shower Parameters

Within VINCIA, initial-state showers refer to any branching type that involves an initial-state parton, ie both II and IF branchings. Note also that the latter is not divided up onto separate IF and FI terms as would be the case in eg Catani-Seymour dipole showers.

Main ISR Switches

flag Vincia:doISR (default = on)
Main switch for initial-state radiation (II and IF antennae) on/off.

flag Vincia:convertGluonToQuark (default = on)
Allow incoming gluons to backwards-evolve into (anti)quarks during the initial-state shower evolution.

flag Vincia:convertQuarkToGluon (default = on)
Allow incoming (anti)quarks to backwards-evolve into (anti)quarks during the initial-state shower evolution.

Factorisation Scale Interpretation (Wimpy vs Power Showers)

Similarly to PYTHIA, for processes that include at least one quark, gluon, or photon in the final state, the default choice in VINCIA is to start the shower from the factorisation scale used for the hard process (as given by PYTHIA for internal processes, or defined by the scale value for Les Houches input),while processes that do not include any such partons are allowed to populate the full phase space. This behaviour can be changed by the following option, which is anologous to the SpaceShower:PTmaxMatch option in PYTHIA.

mode Vincia:pTmaxMatch (default = 0; minimum = 0; maximum = 2)

option 0 : Showers off processes that include at least one final-state quark, gluon, or photon, are started at the factorisation scale, while processes that do not include any such partons are started at the phase-space maximum.
option 1 : Showers are always started at the factorisation scale.
option 2 : Showers are always started at the phase-space maximum. This option is not recommended for physics runs as it will lead to unphysical double counting in many cases.

When the first branching is limited by the factorisation scale for the hard process, a multiplicative factor can be applied to either increase or decrease the shower starting scale relative to the factorisation scale:

parm Vincia:pTmaxFudge (default = 1.0; minimum = 0.1; maximum = 10.0)

parm Vincia:pTmaxFudgeMPI (default = 1.0; minimum = 0.1; maximum = 10.0)
Same as above but for MPI systems, affecting the underlying event.

Note that for any (combination of) choices that result in ISR showers not using the factorisation scale as the starting scale, the generated Sudakov factor will effectively produce leftover PDF ratios in the exclusive cross sections produced by the shower.

mode Vincia:pTdampMatch (default = 2; minimum = 0; maximum = 1)
These options only take effect when a process is allowed to radiate up to the kinematical limit by the above pTmaxMatch choice, and no matrix-element corrections are available. Then, in many processes, the fall-off in pT will be too slow by one factor of pT^2. That is, while showers have an approximate dpT^2/pT^2 shape, often it should become more like dpT^2/pT^4 at pT values above the scale of the hard process. Whether this actually is the case depends on the particular process studied, e.g. if t-channel gluon exchange is likely to dominate. If so, the options below could provide a reasonable high-pT behaviour without requiring higher-order calculations.
option 0 : emissions go up to the kinematical limit, with no special dampening.
option 1 : emissions go up to the kinematical limit, but dampened by a factor k^2 QF^2/(pT^2 + k^2 QF^2), where QF is the factorization scale and k is a multiplicative fudge factor stored in pTdampFudge below.
option 2 : (NOTE: this option has a different meaning in VINCIA than the corresponding ones do in PYTHIA): emissions go up to the kinematical limit, but dampened by a factor k^2 sAnt^2/(pT^2 + k^2 sAnt^2), where sAnt = 2pI.pK is the invariant-mass measure for the emitting antenna, k is a multiplicative fudge factor stored in pTdampFudge below.

parm Vincia:pTdampFudge (default = 1.0; minimum = 0.25; maximum = 4.0)
In cases 1 and 2 above, where a dampening is imposed at around the factorization or antenna-mass scale, respectively, this allows the pT scale of dampening of radiation by a half to be shifted by this factor relative to the default QF or sAnt. This number ought to be in the neighbourhood of unity, but variations away from this value could do better in some processes.

Colour Charge Factors

For theory tests, individual antenna functions can be switched off by setting the corresponding colour-charge factor to zero.

parm Vincia:QQemitII:chargeFactor (default = 2.66666667)
Emission of a final-state gluon from an initial-state qqbar pair.

parm Vincia:GQemitII:chargeFactor (default = 2.83333333)
Emission of a final-state gluon from an initial-state qg (or gqbar) pair.

parm Vincia:GGemitII:chargeFactor (default = 3.0)
Emission of a final-state gluon from an initial-state gg pair.

parm Vincia:QXSplitII:chargeFactor (default = 1.0)
Quark in the initial state backwards evolving into a gluon and emitting an antiquark in the final state

parm Vincia:GXConvII:chargeFactor (default = 2.66666667)
Gluon in the initial state backwards evolving into a quark and emitting a quark in the final state (gluon conversion)

parm Vincia:QQemitIF:chargeFactor (default = 2.66666667)
Gluon emission of an initial-final qq pair

parm Vincia:GQemitIF:chargeFactor (default = 2.83333333)
Gluon emission off an initial-final gq pair

parm Vincia:QGemitIF:chargeFactor (default = 2.83333333)
Gluon emission of an initial-final qg pair

parm Vincia:GGemitIF:chargeFactor (default = 3.0)
Gluon emission of an initial-final gg pair

parm Vincia:QXSplitIF:chargeFactor (default = 1.0)
Quark in the initial state evolving backwards into a gluon and emitting an antiquark in the final state

parm Vincia:GXConvIF:chargeFactor (default = 2.66666667)
Gluon in the initial state backwards evolving into a quark and emitting a quark into the final state (gluon conversion)

parm Vincia:XGSplitIF:chargeFactor (default = 1.0)
Gluon splitting in the final state

Evolution Variable(s)

Choice of functional form of the shower evolution variable (a.k.a. ordering variable) for initial state radiation (see illustrations below).

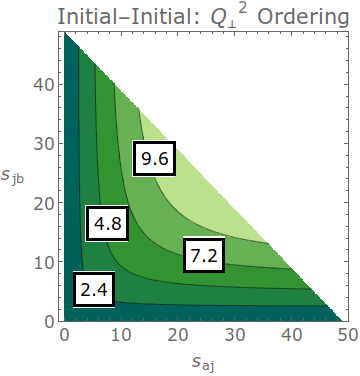
Gluon emissions in initial-initial antennae are ordered in transverse momentum. This evolution variable is the physical (lightcone) transverse momentum for massless partons:

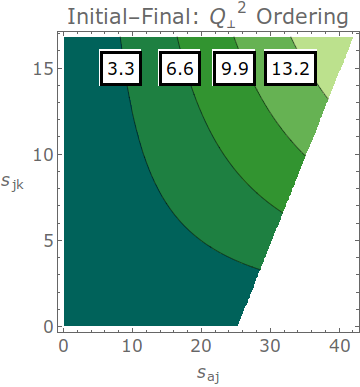
Gluon emissions in initial-final antennae are ordered in transverse momentum. This evolution variable is defined as:

Splittings and conversion in initial-initial and initial-final antennae are by default ordered in the invariant mass of the gq, qq, or qqbar pair respectively. However there is the option to switch to the above transverse momentum ordering by switching Vincia:evolveAllInPT to on. Note that with transverse momentum ordering the ordering variable is no longer the inverse of the singularity associated with the branching process. Also the mass corrections are not applied correctly since they rely on ordering in invariant mass.

flag Vincia:evolveAllInPT (default = off)

The contours below illustrate the progression of the evolution variable over the dipole-antenna phase space for four fixed values, with sAB=mH^2 for the initial-initial case and xA=0.6 and sAK=25.2 GeV^2 for the initial-final case.

Kinematics and Recoils for II Antennae

The post-branching momenta are fixed by the following requirements:
1) The direction of the initial state partons is aligned with the beam axis (z-axis).
2) The invariant mass and the rapidity of the final state recoiler are not changed by the branching. This allows a direct construction of the post-branching momenta in the lab frame.

Kinematics and Recoils for IF Antennae

For IF branchings, Vincia contains implementations of two different kinematics maps, called "local" and "global" in what follows.

In the "local map", the initial-state parton recoils longitudinally, and there is no recoil imparted to any partons that do not participate directly in the branching. (I.e., recoil effects are absorbed locally within the branching antenna, and no partons outside of it are affected.) This is equivalent to saying that any transverse momentum associated with the emitted parton (j) is absorbed by the other final-state parton (k). This allows a simple construction of the post-branching momenta in the centre-of-mass frame of the initial-final antenna.

The "global map" allows for an overall transverse recoil associated with the initial-state leg to be imparted to the system of final-state partons other than those participating directly in the branchings. This is equivalent to saying that any transverse momentum associated with the emitted parton (j) is absorbed by the initial-stage leg (a), after which a Lorentz transformation brings it (plus the final-state system) back to having beam-collinear kinematics. The recoil vanishes For final-state collinear kinematicsbut is in general nonzero outside that limit.

Intuitively, the local map should be appropriate for final-state splittings, while the global one would be appropriate for initial-state ones. The full story is more complicated, partly since soft wide-angle radiation intrinsically represents interference between the two cases, and partly because the phase-space limits for the two maps (outside of the strict soft and collinear limits) are different. (The x < 1 constraint translates to slightly different constraints on the branching invariants for the two maps, as does positivity of the Gram determinant.) A probabilistic selection is therefore made between the local and global maps, using a form obtained by R. Verheyen based on comparisons to DIS matrix elements, P(global) = (sAK - saj)^2/[ (sAK + sjk)^2 + (sAK - saj)^2 ] * Theta( sAK - saj ), with Theta the unit step function (since the momenta in the global map always become unphysical for saj > sAK).

mode Vincia:kineMapIF (default = 1; minimum = 1; maximum = 3)

option 1 : Local recoil map.
option 2 : Gluon emissions use a probabilistic selection between the global and local maps. Antennae that only contain initial-state singularities always use the global one. Antennae that only contain final-state singularities always use the local one.
option 3 : Probabilistic selection between the global and and local maps, for all IF branchings irrespective of their singularity structure.

When using the probabilistic selection, it is possible (in phase-space regions well away from the strict soft and collinear limits) that the selected kinematics map produces unphysical momenta (with x > 1 or negative energies) for the given branching invariants, while the other map would give physical momenta. In such cases, one has to choose whether the given phase-space point should be vetoed, or whether the other map should be allowed to be used instead to construct the kinematics.

flag Vincia:kineMapIFretry (default = off)

option off : If the map selected according to the probabilistic choice above returns unphysical momenta, the trial branching is vetoed.
option on : If the map selected according to the probabilistic choice above returns unphysical momenta, the other map is tried. Only if both maps fail to produce physical momenta is the trial branching vetoed.

Subleading Colour & Colour Reconnections (CR)

During the perturbative shower evolution, the first aspect of subleading colour is simply what colour factors are used for the antenna functions. In a strict leading-colour limit, one would use CA for all antennae, thus overestimating the amount of radiation from quarks (note that we use a normalisation convention in which the colour factor for quarks is 2CF, hence the difference is explicitly subleading in colour). A more realistic starting point is to use 2CF for quark-antiquark antennae, CA for gluon-gluon ones, and something inbetween for quark-gluon ones. Alternatively, a more sophisticated treatment is under development, which exploits QED-like factorisation properties of multi-gluon amplitudes beyond LC. The following switch determines whether and how subleading-colour corrections are treated in the evolution:

mode Vincia:modeSLC (default = 2; minimum = 0; maximum = 3)

option 0 : Strict LC evolution. All gluon-emission colour factors are forced equal to CA thus overcounting the radiation from quarks. Note that matrix-element corrections, if applied at full colour, will still generate corrections to the evolution up to the matched number of legs.
option 1 : Simple Colour Factors. The chargeFactor parameters for each of the antenna functions are used to set the colour factor for each type of gluon-emission antenna; see the section on antenna functions. (Typically, 2CF for qqbar antennae, CA for gg antennae, and the average of 2CF and CA for qg antennae.)
option :
option 2 : Sophisticated Colour Factors. The colour factor for quark-antiquark antennae is forced equal to 2CF. Quark-gluon and gluon-gluon antennae both start out normalised to CA, but a phase-space (and helicity-) dependent correction proportional to -1/NC^2 is applied to QG antennae, containing the collinear parts of a corresponding Q-Qbar antenna. This can be viewed as interpolating between a colour factor of 2CF for radiation collinear with the quark and one proportional to CA for radiation collinear with the gluon.
option 3 : Sophisticated Colour Factors and QCD Multipoles. As for option 2, but also quadrupole (and higher multipole) radiation patterns are allowed as well, starting at order 1/NC^2 for radiation from hard-parton configurations containing at least a q-qbar pair plus two gluons. These patterns are based on the soft limits of subleading-colour amplitudes in QCD, combined with colour-algebra arguments. UNDER DEVELOPMENT.

Colour Flow and Colour Indices

Colour flow is traced using Les-Houches style colour tags, augmented by letting the last digit encode the "colour index", running from 1 to 9, described further in the section below on antenna swing. One ambiguity arises in gluon emission as to which of the daughter antennae should inherit the "parent" colour tag/index, and which should be assigned a new one. This is controlled by the following parameter:

mode Vincia:CRinheritMode (default = 1; minimum = -2; maximum = 2)

option 0 : Random
option 1 : The daughter with the largest invariant mass has a probability 1/(1 + r) to inherit the parent tag, with r < 1 the ratio of the smallest to the largest daughter invariant masses squared.
option 2 : The daughter with the largest invariant mass always inherits the parent tag (winner-takes-all extreme variant of option 1).
option -1 : (Unphysical, intended for theory-level studies only). Inverted variant of option 1, so that the daughter with the smallest invariant mass preferentially inherits the parent colour tag.
option -2 : (Unphysical, intended for theory-level studies only). Inverted variant of option 2, so that the daughter with the smallest invariant mas always inherits the parent colour tag.

VINCIA's Model of Non-perturbative Antenna/String Reconnections

In QCD, the probability that a random quark and a random antiquark are in an overall singlet state is given by the colour algebra:

3 ⊗ 3bar = 1 ⊕ 8

From colour counting alone, any pair of random (colour-disconnected) triplet-antitriplet charges should thus have a 1/9 probability to be in an overall singlet state. Following the approach in ARIADNE, this can be represented by assigning to every leading-colour antenna an index running from 1 to 9 and allowing reconnections to occur only between ones having the same such index. To ensure that the octet nature of gluons is respected, the assignment of indices is restricted so that neighbouring antennae, and quark pairs originating directly from g→qq splittings, always have different indices. Next-to-nearest neighbours in colour space are treated as completely colour-disconnected in the context of this model.

The next question to be addressed is what is the dynamics of the reconnections. From coherence and by analogy with QED (having dealt with the colour-factor suppression above), we expect something like a principle of maximal screening. In an angular-ordering context, this can be illustrated by imagining a system of several colour and anti-colour charges all having the same index. Maximal destructive interference would then imply that the radiation cone around each colour-charged parton should be set up so as to extend to the nearest (in angle) same-index anticolour charge, regardless of the leading-colour connections and keeping in mind that each anticolour charge can only cancel one unit of colour charge.

In a non-perturbative context, and specifically with the Lund string model in mind, the relevant measure for judging which antennae are "closest" to each other is the string length measure, Λ, which is given by the invariant mass of the string piece endpoints:

Λ(pa,pb) = (pa+pb)² - (ma+mb)² = 2*(pa.pb) - 2*ma*mb

where the subtraction of the sum of endpoint masses ensures that a "string" spanned by two massive particles at rest is assigned zero length.

Thus, for two same-index antennae spanned between the four parton momenta (p1,p2) and (k1,k2), we may compare the two string lengths:

Λ₁ = Λ(p1,p2) * Λ(k1,k2)
Λ₂ = Λ(p1,k2) * Λ(k1,p2)

Note that both expressions are linear in each of the participating momenta, so the choice only depends on the directions of motion of the involved partons.

The current implementation of non-perturbative swing in VINCIA is deterministic: among same-index antennae, the configuration with the smallest Λ always wins. The model therefore currently has no free parameters, apart from a minimum mass-squared of order (1 GeV)² which is imposed when comparing the configurations, see Parameters and Switches below. The actual measure that is minimized by the algorithm is therefore

Λ_eff(pa.pb) = Λ(pa,pb) + m_min²

with m_min a regulator expressing the fact that infinitely soft and collinear gluons do not lead to zero-mass string pieces but are instead smoothly absorbed into a physical string of hadronic dimensions. We emphasize that the minimal-mass parameter is only added for the purpose of calculating the Λ measure, without touching the parton momenta themselves. If a small-mass reconnection still wins, despite the m_min penalty, then the corresponding topology is accepted. However, the Lund string model then ensures that any small invariant is smoothly absorbed into the string, as desired. Physically, one should in these cases probably instead compute the overall string measure obtained by clustering the small-invariant momenta together, rather than treating them as separate partons, a sophistication that would introduce corrections like

m_min² → m_min² ( 1 + min[ Λ(p,k_R)/Λ(k,k_R) , Λ(p_L,k)/Λ(p_L,p) ]

with p_L and k_R the colour neighbours (of p and k, respectively) of the reconnected small-invariant antenna spanned by (p,k). This last level of sophistication, however, has not been implemented in VINCIA's CR algorithm so far.

Though the model presented here thus has no free parameters (beyond the minimal-mass parameter), for completeness, we note that the corresponding implementation in ARIADNE makes a stochastic selection, with a variable strength.

If there are several possible reconnections to choose between (more than two antennae with the same colour index), VINCIA creates a matrix of dot products, in which the diagonal represents the colour-connected invariants. It then iteratively minimizes the product of diagonal entries by successive column swaps, starting from the largest entry on the diagonal and working downwards until no more swaps would result in a reduction of the overall Λ measure. (We neglect the small risk that this procedure could end up trapped in a local minimum; a possibility that could eventually be overcome by applying stochastic methods and/or by considering higher-than-binary column rearrangements).

Note that this model is only intended to reflect the coherence expected from colour screening. The possibility of additional nonperturbative dynamics, for instance that strings or hadrons, once formed, could rescatter, fuse, or cut each other up, is not explicitly addressed.

Baryon Junctions

A further intriguing possibility that opens up at subleading colour is the formation of colour-epsilon (and corresponding anticolour-epsilon) structures in the colour field. In the colour algebra, this first appears when considering the combination of two random same-sign colour triplets:

3 ⊗ 3 = 3bar ⊕ 6

where the sextet corresponds to a configuration that can be treated as unreconnected (in analogy with the octet in the formula for triplet-antitriplet combinations above), but the 3bar corresponds to the coherent addition of two colour triplets to form an effective antitriplet (e.g., red + green can look antiblue seen from a distance). In non-perturbative terms, this is represented as a diquark (if the invariant mass is of hadronic size) or, more generally, a string junction, see [Sjö03]. Both carry baryon number, and hence this mechanism provides a new and interesting possibility for baryon formation. This has traditionally been a weak point in the Lund string formalism, so even modest improvements would be welcome. In particular, junctions produce less strong baryon-antibaryon correlations (than the standard mechanism of diquark-pair string breaks), due to separation in both flavour and phase space of the produced baryons and antibaryons.

Interestingly, the colour-factor suppression is here only 3/(3+6) = 1/NC, rather than 1/NC². This is enough to allow a system of two charges and two anticharges to reconnect into a junction-antijunction configuration. (In general, one may consider also cases in which the junction is not connected directly to the antijunction, instead connecting to it via an arbitrary number of gluons, in which case the accident would have to happen twice, once at each end, a higher-order possibility we so far do not consider in this model.)

For the special case of systems that are neighbors in colour space (eg the quarks in Z→qqq̅q̅), the fact that neighbouring colours cannot be identical (due to the octet nature of gluons) leaves only the 6 combinations of non-identical colours our of the total 9 in the formula for triplet-triplet combinations above, of which half are antisymmetric (the 3bar). Thus, in this particular case, the suppression factor is only 1/2.

Though a perturbative formulation could be possible, we shall here restrict our attention to junction formation at the non-perturbative transition stage. This is partly due to the fact that perturbative radiation from colour-epsilon configurations has not yet been implemented in VINCIA. (In a perturbative framework a la angular ordering, one would presumably treat wide-angle radiation coherently, with the 3bar, but small-angle radiation - inside the opening angle of the two triplets - incoherently.)

The relevant string measure for comparing a 0-junction and a 2-junction topology was derived in [Sjö03]. Here, we take a simplified approach, considering the junction-junction system as made up of one string piece between two virtual "diquarks" and one piece inside each of the diquarks, thus representing the the total string length by

Λ_2-junction = Λ(p1+p2,k1+k2) * Λ(p1,p2) * Λ(k1,k2)
Λ_0-junction = Λ(p1,k1) * Λ(p2,k2)

where (p1,k1) and (p2,k2) are the two original (unreconnected) antennae, with p1 and p2 the momenta of the colour charges and k1 and k2 those of the anticolour charges. Due to the different dimension of the two expressions (one involves three string pieces, the other only two), there is here an explicit dependence on the normalisation of the Λ measure, which we denote m₀, expected to be roughly of order 1 GeV. We take this parameter to be independent of the m_min value introduced in Λ_eff above, so that the actual measures to be compared are:

Λ_2-junction = [ Λ_eff(p1+p2,k1+k2) * Λ_eff(p1,p2) * Λ_eff(k1,k2) ] / m_0;⁶
Λ_0-junction = [ Λ_eff(p1,k1) * Λ_eff(p2,k2) ] / m_0;⁴

Due to the different powers of m₀, large m₀ values will increase the amount of 2-junction topologies that "win" (i.e., have the smallest Λ measure).

Since we are not technically able to treat systems with more than a single junction-antijunction connection, we impose that only antennae taken from two different q-q̅ chains are able to reconnect to junctions. Physically, this also reflects that it should be likely for the two junctions in a system with two (or even three) strings spanned between the same junction and antijunction to annihilate, thus reverting to the original non-junction colour flow. Likewise, antennae residing inside gluon loops are not given the possibility of participating in junction reconnections.

Simplifying the colour arguments above slightly, we allow reconnections to occur between antennae with different-parity antenna indices (that is, e.g., junction reconnections will be allowed between (1,2) but not between (1,3). In particular, this projects out the same-index case and only keeps half of the remaining 8 possibilities. The generic colour suppression factor for reconnections involving junctions thus comes out to 4/9, instead of 3/9, but we consider this an acceptable margin of error, especially since the restrictions imposed will cause some possibilities to not be tried at all, and the free parameter m₀ gives a possibility to further adjust the overall strength of junctions reconnections. We note, however, that for the special case of nearest-neighbours, the probability for different-parity indices is 4/8 = 1/2, as desired (the same-index case never occurs for nearest neighbours).

Switches and Parameters for VINCIA's CR Model

flag Vincia:doCR (default = off)

The m_min parameter in the expression for the effective Λ measure above is given by:

parm Vincia:CRmMin (default = 1.0; minimum = 0.0)

The possibility of junction formation at the non-perturbative stage is regulated by the following switch:

flag Vincia:CRjunctions (default = off)

The dimensionful scale normalizing the measure for junction reconnections is set by:

parm Vincia:CRjunctionsM0 (default = 2.0; minimum = 0.1; maximum = 10.0)

QCD Shower Cutoffs and Hadronisation

It is possible to pass the parton systems produced by VINCIA through PYTHIA's string hadronisation model. Normally, this should happen automatically, according to the setting of the PYTHIA switch HadronLevel:all. The main parameter from the shower side is then the phase-space contour defined by the hadronisation cutoff.

The hadronisation cutoff, a.k.a. the infrared regularisation scale, defines the resolution scale at which the perturbative shower evolution is stopped. Thus, perturbative emissions below this scale are treated as fundmanentally unresolvable and are in effect inclusively summed over.

Important Note: when hadronisation is switched on, there is a delicate interplay between the hadronisation scale used in the shower and the parameters of the hadronisation model. Ideally, the parameters of the hadronisation model should scale as a function of the shower cutoff. This scaling does not happen automatically in current hadronisation models, such as the string model employed by PYTHIA. Instead, the parameters of the hadronisation model are tuned for one specific shower setting at a time and should be retuned if changes are made to the shower cutoff.

Cutoff Scale

parm Vincia:cutoffScaleFF (default = 0.75)
This parameter sets the value (in GeV) of the final state shower cutoff. For evolutionType = 1 it is interpreted as a cutoff on ARIADNE pT, while for evolutionType = 2 it is interpreted as a cutoff on invariant mass.

parm Vincia:cutoffScaleII (default = 0.75)
This parameter sets the value (in GeV) of the shower cutoff for initial-initial antennae.

parm Vincia:cutoffScaleIF (default = 0.75)
This parameter sets the value (in GeV) of the shower cutoff for initial-final antennae.

Settings for the QED shower

Main Switches

flag Vincia:doQED (default = on)
Main switch for QED evolution on/off.

mode Vincia:nGammaToQuark (default = 5; minimum = 0; maximum = 6)
Number of allowed quark flavours in final-state photon splitting.

mode Vincia:nGammaToLepton (default = 3; minimum = 0; maximum = 3)
Number of allowed lepton flavours in final-state photon splitting.

flag Vincia:convertGammaToQuark (default = on)
Allow incoming photons to backwards-evolve into (anti)quarks during the initial-state shower evolution.

flag Vincia:convertQuarkToGamma (default = on)
Allow incoming (anti)quarks to backwards-evolve into photons during the initial-state shower evolution.

The QED coupling in the Vincia Shower

mode Vincia:alphaEMorder (default = 1; minimum = 0; maximum = 1)

option 0 : zeroth order, i.e. α_em is kept fixed.
option 1 : first order, i.e., one-loop running.

parm Vincia:alphaEM0 (default = 0.00729735; minimum = 0.0072973; maximum = 0.0072974)
The alpha_em value at vanishing momentum transfer (and also below m_e).

parm Vincia:alphaEMmZ (default = 0.00781751; minimum = 0.00780; maximum = 0.00783)
The alpha_em value at the M_Z mass scale.

Lower Cutoffs for the QED evolution

parm Vincia:QminChgQ (default = 0.5; minimum = 0.1; maximum = 2.0)
Parton shower cut-off scale for photon coupling to coloured particle.

parm Vincia:QminChgL (default = 1e-6; minimum = 1e-10; maximum = 2.0)
Parton shower cut-off scale for pure QED branchings. Assumed smaller than (or equal to) QminChgQ.

Other QED Settings

mode Vincia:photonEmissionMode (default = 1; minimum = 1; maximum = 2)

option 1 : Pairing algorithm
option 2 : Coherent algorithm

flag Vincia:fullWkernel (default = on)
Switch to incorporate the full antenna function for W radiation. If disabled, a W radiates as if it were a lepton.

parm Vincia:mMaxGamma (default = 10.; minimum = 0.001; maximum = 5000.0)
Maximum invariant mass allowed for the created fermion pair by photon splitting in the shower.

Evolution with Enhanced (Biased) Kernels

VINCIA's shower evolution can be biased to populate the multi-jet phase space more efficiently and/or enhance the rate of rare processes such as g→bb and g→cc splittings. It is also possible to inhibit radiation (e.g., to focus on Sudakov regions), by choosing enhancement factors smaller than unity. When these options are used, it is important to note that the event weights will be modified, reflecting that some types of events (e.g., multijet events, or events with gluon splittings to heavy quarks) will be "overrepresented" statistically, and others (events with few jets, or events with no gluon splittings to heavy quarks) underrepresented. Averages and histograms will therefore only be correct if computed using the correct weight for each generated event. A description and proof of the algorithm can be found in [MS16]. Note that care has been taken to ensure that the weights remain positive definite; under normal circumstances, VINCIA's enhancement algorithm should not result in any negative weights.

flag Vincia:enhanceInHardProcess (default = on)
This flag controls whether the enhancement factors are applied to shower branchings in the hard-process system.

flag Vincia:enhanceInResonanceDecays (default = on)
This flag controls whether the enhancement factors are applied to shower branchings inside resonance-decay systems (like Z/W/H decays) that are treated as factorised from the hard process.

flag Vincia:enhanceInMPIshowers (default = off)
This flag controls whether the enhancement factors are applied to shower branchings in MPI systems.

parm Vincia:enhanceFacAll (default = 1.0; minimum = 0.01; maximum = 100.0)
This enhancement factor is applied as a multiplicative factor common to all antenna functions, increasing the likelihood of all shower branchings by the same amount. Values greater than unity thus more frequently yields "busy" events, with many shower branchings. Values smaller than unity suppress additional branchings, yielding more Sudakov-like events.

parm Vincia:enhanceFacBottom (default = 1.0; minimum = 1.0; maximum = 100.0)
This enhances the probability for all branchings that increase the number of bottom quarks (i.e., FSR g→bb splittings and the corresponding ISR flavour-excitation process). Note: this factor is applied on top of Vincia:biasAll.

parm Vincia:enhanceFacCharm (default = 1.0; minimum = 1.0; maximum = 100.0)
Same as Vincia:enhanceFacBottom but for charm quarks. Note: this factor is applied on top of Vincia:biasAll.

parm Vincia:enhanceCutoff (default = 10.0; minimum = 0.0; maximum = 1000.0)
Do not apply enhancement factors to branchings below this scale. Intended to be used to focus on enhancements of hard branchings only.

Shower Uncertainty Bands

A calculation is only as good as the trustworthiness of its uncertainty bands. Although not foolproof, VINCIA attempts to make comprehensive and explicit estimates of the theoretical accuracy of the answers it provides, event by event in phase space. Obviously, VINCIA can only make these estimates for the parts of the calculation that it handles itself - hence the automatic uncertainty estimates are currently limited to the perturbative parts of the calculation.

When switched on, the uncertainty variations are provided as, and can be accessed by the user through, a vector of alternative weights that is provided for each event. If the event is in a phase space region that VINCIA believes to be under good perturbative control (according to the showering and matching criteria specified by the user), the spread in weights will be small, whereas it will be larger for events populating less well controlled phase space regions.

Since the uncertainty estimate is fully differential in phase space, cuts can be imposed post facto without causing any special problems. E.g., if the cuts isolate a poorly controlled region, all the accepted events will have relatively large event weight spreads, and hence the overall relative uncertainty will increase, as expected.

Needless to say, these uncertainties still have to be interpreted with caution, but due to a large amount of flexibility in the VINCIA formalism, VINCIA can perform quite a few variations that are not possible with other generators. We therefore believe that the uncertainties quoted by VINCIA are, at least, reasonably meaningful.

Note also that the "central" set of weights (corresponding to the settings chosen by the user for the current run) is normally unweighted by default in VINCIA. I.e., all the events have identical weights and can be trivially added together statistically. The uncertainty weight sets are computed in such a way that this still holds true on average for each uncertainty variation individually. I.e., although the weights corresponding to uncertainty variation n fluctuate about unity, event to event, their average over many events will still be unity. Formally, this is due to the variations being done in a way that conserves unitarity. Practically, it means that none of the variations change the input total (Born-level) normalisation - they only change how it is distributed across phase space. The user should therefore be aware that there can still be an overall "K" factor, not addressed by these uncertainty bands.

The speed of the calculation is not significantly affected by adding uncertainty variations, but the code does run slightly faster without them. We therefore advise to keep them switched off whenever they are not going to be used. See speed below for more on the impact on performance.

Note that the variations in VINCIA are similar to the ones included in Pythia. The set of switches and parameters is therefore similar to what is available in Pythia.

Note that the variations only represent variations of the perturbative shower parameters. Since VINCIA does not handle the non-perturbative phase of fragmentation, uncertainty estimates for parameters related to that part must still be performed in the traditional way. Especially for infrared sensitive observables, the user is therefore advised to carry out separate variations of the non-perturbative parameters, such as the a and b parameters of the Lund symmetric fragmentation function and of other hadronisation and hadron decay parameters that may be of relevance to the study at hand.

VINCIA provides a possibility for evaluating the variations described above automatically. For every event it generates, it will then tell you the effective spread of weights it found for that particular phase space point, which saves you the effort to make separate additional runs, one for each variation. It also saves computing time, since the uncertainty evaluation only mildly affects the overall speed of the generator.

Automated Uncertainties On/Off

flag Vincia:uncertaintyBands (default = off)
Main switch for VINCIA's automatic evaluation of theoretical uncertainty bands. When set to on VINCIA internally keeps track of several variations of the shower approximation and outputs a vector of weights for each event.

By default, the automated shower uncertainty variations are enabled for the showers off the hardest interaction (and associated resonance decays), but not for the showers off MPI systems which would be more properly labeled as underlying-event uncertainties. If desired, the variations can be applied also to showers off MPI systems via the following switch:

flag Vincia:uncertaintyInMPIshowers (default = off)
Flag specifying whether the automated shower variations include showers off MPI systems or not. Note that substantially larger weight fluctuations must be expected when including shower variations for MPI, due to the (many) more systems which then enter in the reweightings.

UserHooks Warning: the calculation of uncertainty variations will only be consistent in the absence of any external modifications to the shower branching probabilities via the UserHooks framework. It is therefore strongly advised to avoid combining the automated uncertainty calculations with any such UserHooks modifications.

Merging Warning: in multi-jet merging approaches, trial showers are used to generate missing Sudakov factor corrections to the hard matrix elements. Currently that framework is not consistently combined with the variations introduced here, so the two should not be used simultaneously.

Specifying the Variations

When Vincia:uncertaintyBands is switched on, the user can define an arbitrary number of (combinations of) uncertainty variations to perform. Each variation is defined by a string with the following generic format:

 
    label keyword1=value keyword2=value ...

The user has complete freedom to specify the label, and each keyword must be selected from the list below.

Once a list of variations defined as above has been decided on, the whole list should be passed to Pythia/VINCIA in the form of a single vector of strings, defined as follows:

wvec Vincia:UncertaintyBandsList (default = {alphaShi ff:muRfac=0.5 if:muRfac=0.5 ii:muRfac=0.5, alphaSlo ff:muRfac=2.0 if:muRfac=2.0 ii:muRfac=2.0, hardHi ff:cNS=2.0 if:cNS=2.0 ii:cNS=2.0, hardLo ff:cNS=-2.0 if:cNS=-2.0 ii:cNS=-2.0})
Vector of uncertainty-variation strings defining which variations will be calculated by VINCIA when Vincia:uncertaintyBands is switched on.

The following list includes all keywords that can currently be processed:

ff:muRfac : multiplicative factor applied to the renormalization scale in GeV for FF branchings.
if:muRfac : multiplicative factor applied to the renormalization scale in GeV for IF branchings.
ii:muRfac : multiplicative factor applied to the renormalization scale in GeV for II branchings.
ff:cNS : additive non-singular ("finite") term in the FF splitting functions (applied as +ff:cNS/sIK).
if:cNS : additive non-singular ("finite") term in the IF splitting functions (applied as +if:cNS/sAK).
ii:cNS : additive non-singular ("finite") term in the II splitting functions (applied as +ii:cNS/sAB).

Optionally, a further level of detail can be accessed by specifying variations for specific types of branchings, with the global keywords above corresponding to setting the same value for all branchings. Using the if:muRfac parameter for illustration, the individual branching types that can be specified are:

if:QQemit:muRfac : variation for gluon emission off initial-final qq pair.
if:GQemit:muRfac : variation for gluon emission off initial-final gq pair.
if:QGemit:muRfac : variation for gluon emission off initial-final qg pair.
if:GGemit:muRfac : variation for gluon emission off initial-final gg pair.
if:QXsplit:muRfac : variation for an initial state quark backwards evolving into a gluon and emitting an antiquark in the final state.
if:GXconv:muRfac : variation for an initial state gluon backwards evolving into a quark and emitting a quark in the final state.
if:XGsplit:muRfac : variation for a gluon splitting in the final state.

Similarly defined are ii:QQemit:muRfac, ii:GQemit:muRfac, ii:GGemit:muRfac, ii:QXsplit:muRfac, ii:GXconv:muRfac, ff:QQemit:muRfac, ff:QGemit:muRfac, ff:GGemit:muRfac, and ff:XGsplit:muRfac.

To exemplify, an uncertainty variation corresponding to simultaneously increasing both the ISR and FSR renormalisation scales by a factor of two would be defined as follows

 
    alphaSlo ff:muRfac=2.0 if:muRfac=2.0 ii:muRfac=2.0

Different histograms can then be filled with each set of weights as desired (see accessing the uncertainty weights below). Variations by smaller or larger factors can obviously also be added in the same way, again within one and the same run.

The main intended purpose of these variations is to estimate perturbative uncertainties associated with the parton showers. Due to the pole at LambdaQCD, however, branchings near the perturbative cutoff can nominally result in very large reweighting factors, which is unwanted for typical applications. We therefore enable to limit the absolute (plus/minus) magnitude by which alphaS is allowed to vary by

parm Vincia:deltaAlphaSmax (default = 0.2; minimum = 0.0; maximum = 1.0)
The allowed range of variation of alphaS, interpreted as abs(alphaSprime - alphaS) < deltaAlphaSmax.

Likewise, non-singular-term variations are mainly intended to capture uncertainties related to missing higher-order tree-level matrix elements and are hence normally uninteresting for very soft branchings. The following parameter allows to switch off the variations of non-singular terms below a fixed perturbative threshold:

parm Vincia:cNSpTmin (default = 5.0; minimum = 0.0; maximum = 20.0)
Variations of non-singular terms will not be performed for branchings occurring below this threshold.

Additionally, there is a run-time parameter:

flag Vincia:muSoftCorr (default = on)
This flags tells the shower to apply an O(αS²) compensation term to the renormalization-scale variations, which reduces their magnitude for soft emissions.

No uncertainty variations at all will be calculated below the following scale

parm Vincia:uncertaintyBandsCutoff (default = 2.0; minimum = 0.0)
Scale below which uncertainty variations are completely switched off.

Accessing the Uncertainty Bands

The first (zero'th) entry in the vector of event weights always corresponds to the settings chosen by the user, and will normally have weights equal to unity (if showering an unweighted set of events), see the page on weights. If showering a weighted set of events, the nominal (user) weights are propagated through VINCIA and can be obtained through the method

vincia.weight();

The uncertainty bands are represented by alternative sets of weights, where the spread of weights for each indidivual event gives an estimate of how "sure" VINCIA is about the weight for that particular event. Regions of phase space where the theoretical uncertainty is large are thus reflected by large weight spreads, while regions where the shower approximations work well have smaller differences. After showering, the weights corresponding to the uncertainty bands are accessible via the same method as that used for the central weight set, by giving a non-zero index to the weight() method,

vincia.weight(int iVar);

where iVar is an integer code specifying the particular variation you want the weight for. The numbering corresponds to the order of the variations specified above. The number of available variations you can access is given by

vincia.nVariations();

Finally you can access the label of the variation (as specified in Vincia:UncertaintyBandsList) by

vincia.weightLabel(int iVar);

Since the events generated are the same for all the variations, only one event set needs to be passed, e.g., to models for hadronisation and/or detector corrections. The bands are correctly propagated through these models by simply keeping track of the different weight sets and applying these at any stage after the shower evolution has finished. Hence substantial overall speed gains compared to a full-fledged traditional uncertainty estimation should be possible.

VINCIA Tunes

VINCIA accepts input of tune presets in the form of a standard PYTHIA 8 command file whose name and location can be specified by the user.

word Vincia:tuneFile (default = default.cmnd)
Name of a command file (optionally including an absolute or relative path) containing tune presets for VINCIA. If no explicit path is given, the current working directory will be searched first, then the share/Vincia/tunes directory.

Note: the requested file will only be read in when VINCIA is switched on, in order not to interfere with the PYTHIA settings when VINCIA is switched off.

Note 2: a special value for this parameter is "none", in which case no tune file will be used (i.e., PYTHIA's parameters will be used as they are).

Note 3: the entries in the tune file will be superseded by any user modifications made in the main command file given to the VINCIA constructor. This should allow sufficient flexibility to explore user variations away from the tuned values.

A particular set of user-defined parameters can easily be made into a tune set by simply copying the relevant parts of the user's normal command file (i.e., omitting the process-specific and program control parameters) into a new file that can then be shared and/or submitted to the VINCIA authors for possible inclusion in future distributions. In order to make tunings more stable against possible changes in the program defaults (be it PYTHIA or VINCIA), it is advisable to include all relevant parameter values explicitly in the tune file, rather than letting parameters that retain their (version-specific) default values be defined implicitly.

Advice on Tuning

Although there are obviously parameters that it makes more sense to tune than others, there is no explicit restriction imposed on what parameters are allowed to be present in the tune file. This implies some responsibility on the part of the user.

As a guideline, the main parameters that need to be properly tuned are the non-perturbative hadronisation parameters used in PYTHIA's string fragmentation model. Since PYTHIA and VINCIA treat soft radiation somewhat differently, there can be important differences between the two in the soft region that the hadronisation model will not re-absorb automatically and which therefore only a retuning can address.

The strategy used for the default tune of VINCIA is to take the reference value for alphaS from the current world average value in the MSbar scheme, and let the effective shower scheme tuning be done by first translating to the CMW scheme and then fine-tune by modifying the renormalisation-scale prefactors used for shower branchings. However, for best results, be aware that an (N)NLO extraction of alphaS should still ideally be combined with explicit (N)NLO matrix-element corrections to the shower.

An alternative (but equivalent) strategy that is often used in PYTHIA tunes, is to perceive of the value of the strong coupling itself as a tuning parameter. In this case the interpretation is that extracting alphaS from, e.g., event shapes, can be done equally well using a shower code as with more analytical approaches. The difference is that the alphaS value extracted with the shower code is in an a priori unknown scheme, defined by the shower algorithm. If the shower only includes LO/LL accuracy for the given observable(s), the extraction should be compared with other LO/LL extractions. This typically yields alphaS values ~ 0.13 - 0.14. When explicit NLO corrections are included for the relevant observable(s), values comparable to other NLO extractions should result, around 0.12.